重载(Overload)和重写(Override)的区别
方法的重载和重写都是实现多态的方式,区别在于前者实现的是编译时的多态性,而后者实现的是运行时的多态性。
重载:一个类中有多个同名的方法,但是具有有不同的参数列表(参数类型不同、参数个数不同或者二者都不同)。
重写:发生在子类与父类之间,子类对父类的方法进行重写,参数都不能改变,返回值类型可以不相同,但是必须是父类返回值的派生类。即外壳不变,核心重写!重写的好处在于子类可以根据需要,定义特定于自己的行为。
注:
- 重载的概念是:方法名称相同,参数个数、次序、类型不同因此重载对返回值没有要求,可以相同,也可以不同,但是如果参数的个数、类型、次序都相同,方法名也相同,仅返回值不同,则无法构成重载如:
//这2个方法不能构成重载,会有编译错误。
public int A(int i);
public double A(int i);
//这2个方法可以形成重载
public int A(int i);
public double A(double i);不能根据返回类型来区分重载的原因:
- 如果我们有两个方法如下,当我们调用:test(1) 时,编译器无法确认要调用的是哪个。方法的返回值只是作为方法运行之后的一个“状态”,但是并不是所有调用都关注返回值,所以不能将返回值作为重载的唯一区分条件。
// 方法1
int test(int a);
// 方法2
long test(int a);抽象类(abstract class)和接口(interface)的区别
- 抽象类只能单继承,接口可以多实现。
- 抽象类可以有构造方法,接口中不能有构造方法。
- 抽象类中可以有成员变量,接口中没有成员变量,只能有常量(默认就是 public static final)。
- 抽象类中可以包含非抽象的方法,在 Java 7 之前接口中的所有方法都是抽象的,在 Java 8 之后,接口支持非抽象方法:default 方法、静态方法等。Java 9 支持私有方法、私有静态方法。
- 抽象类中的方法类型可以是任意修饰符,Java 8 之前接口中的方法只能是 public 类型,Java 9 支持 private 类型。
设计思想的区别:
接口是自上而下的抽象过程,接口规范了某些行为,是对某一行为的抽象。我需要这个行为,我就去实现某个接口,但是具体这个行为怎么实现,完全由自己决定。
抽象类是自下而上的抽象过程,抽象类提供了通用实现,是对某一类事物的抽象。我们在写实现类的时候,发现某些实现类具有几乎相同的实现,因此我们将这些相同的实现抽取出来成为抽象类,然后如果有一些差异点,则可以提供抽象方法来支持自定义实现。
打个比方:
普通类像亲爹 ,他有啥都是你的。
抽象类像叔伯,有一部分会给你,还能指导你做事的方法。
接口像干爹,可以给你指引方法,但是做成啥样得你自己努力实现。
wait() 和 sleep() 方法的区别
- 来源不同:sleep() 来自 Thread 类,wait() 来自 Object 类。
- 对于同步锁的影响不同:sleep() 不会该表同步锁的行为,如果当前线程持有同步锁,那么 sleep 是不会让线程释放同步锁的。wait() 会释放同步锁,让其他线程进入 synchronized 代码块执行。
- 使用范围不同:sleep() 可以在任何地方使用。wait() 只能在同步控制方法或者同步控制块里面使用,否则会抛 IllegalMonitorStateException。
- 恢复方式不同:两者会暂停当前线程,但是在恢复上不太一样。sleep() 在时间到了之后会重新恢复;wait() 则需要其他线程调用同一对象的 notify()、nofityAll() 才能重新恢复。
为什么要使用线程池?为什么不直接new个线程?
如果我们在方法中直接new一个线程来处理,当这个方法被调用频繁时就会创建很多线程,不仅会消耗系统资源,还会降低系统的稳定性,一不小心把系统搞崩了,就可以直接去财务那结帐了。
如果我们合理的使用线程池,则可以避免把系统搞崩的窘境。总得来说,使用线程池可以带来以下几个好处:
- 降低资源消耗。通过重复利用已创建的线程,降低线程创建和销毁造成的消耗。
- 提高响应速度。当任务到达时,任务可以不需要等到线程创建就能立即执行。
- 增加线程的可管理型。线程是稀缺资源,使用线程池可以进行统一分配,调优和监控。
List、Set、Map
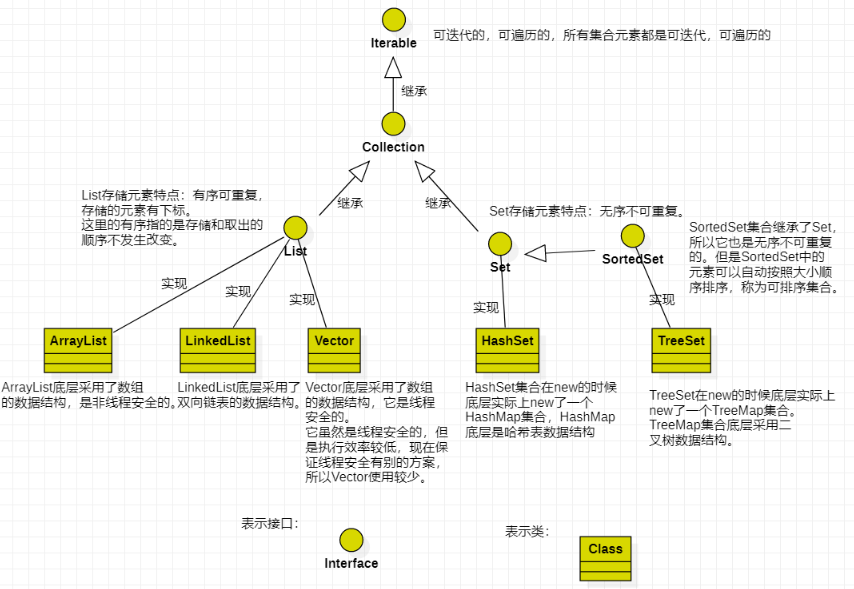
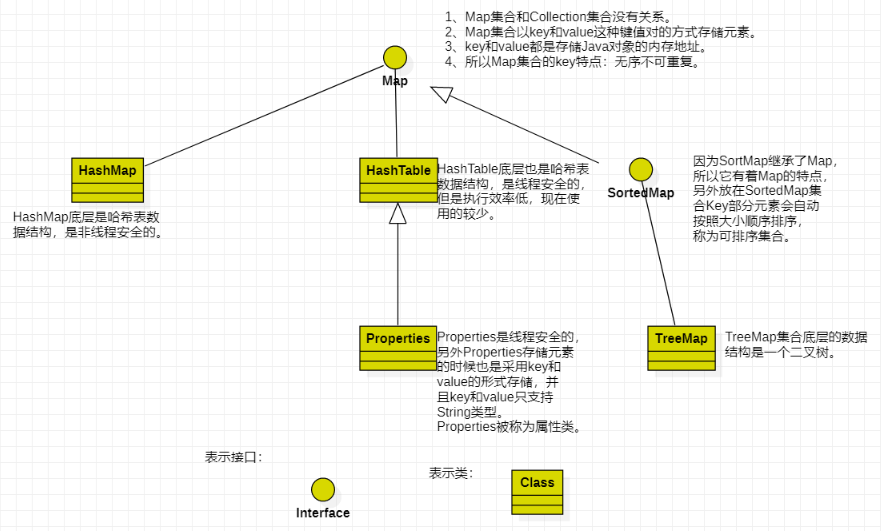
HashMap 和Hashtable 的区别
- HashMap 允许 key 和 value 为 null,Hashtable 不允许。
- HashMap 的默认初始容量为 16,Hashtable 为 11。
- HashMap 的扩容为原来的 2 倍,Hashtable 的扩容为原来的 2 倍加 1。
- HashMap 是非线程安全的,Hashtable是线程安全的。
- HashMap 的 hash 值重新计算过,Hashtable 直接使用 hashCode。
- HashMap 去掉了 Hashtable 中的 contains 方法。
- HashMap 继承自 AbstractMap 类,Hashtable 继承自 Dictionary 类。
类加载的过程
- 类加载的过程包括:加载、验证、准备、解析、初始化,其中验证、准备、解析统称为连接。
- 加载:通过一个类的全限定名来获取定义此类的二进制字节流,在内存中生成一个代表这个类的java.lang.Class对象。
- 验证:确保Class文件的字节流中包含的信息符合当前虚拟机的要求,并且不会危害虚拟机自身的安全。
- 准备:为静态变量分配内存并设置静态变量初始值,这里所说的初始值“通常情况”下是数据类型的零值。
- 解析:将常量池内的符号引用替换为直接引用。
- 初始化:到了初始化阶段,才真正开始执行类中定义的 Java 初始化程序代码。主要是静态变量赋值动作和静态语句块(static{})中的语句。
饿汉模式、懒汉模式和静态内部类(延迟初始化占位类)
饿汉:
//线程安全、非懒加载、效率高。
public class Singleton {
// 1.饿汉
private static Singleton instance = new Singleton();
private Singleton() {}
public static Singleton getInstance() {
return instance;
}
}饿汉模式,比较常见的一种写法。在类加载的时候就对实例进行初始化,没有线程安全问题;获取实例的静态方法没有使用同步,调用效率高;但是没有使用懒加载,如果该实例从始至终都没被使用过,则会造成内存浪费。
懒汉:
//线程安全、懒加载、效率低。
public class Singleton {
// 2.懒汉
private static Singleton instance;
private Singleton() {}
public static synchronized Singleton getInstance() {
if (instance == null) {
instance = new Singleton();
}
return instance;
}
}线程安全的懒汉模式,比较常见的一种写法。在第一次使用的时候才进行初始化,达到了懒加载的效果;由于获取实例的静态方法用synchronized修饰,所以也没有线程安全的问题;但是,这种写法每次获取实例都要进行同步(加锁),因此效率较低,并且可能很多同步都是没必要的。
注:该模式还有另一种常见写法,就是把getInstance方法上的synchronized去掉,这种方法有线程安全问题,不能使用。
静态内部类(延迟初始化占位类):
//线程安全、懒加载、效率高。
public class Singleton {
// 4.静态内部类
private static class Holder {
private static final Singleton INSTANCE = new Singleton();
}
private Singleton() {}
public static final Singleton getInstance() {
return Holder.INSTANCE;
}
}静态内部类(延迟初始化占位类),比较常见的一种写法。JVM将推迟SingletonHolder的初始化操作,直到开始使用这个类时才初始化,并且由于通过一个静态初始化来初始化Singleton,因此不需要额外的同步。当任何一个线程第一次调用getInstance时,都会使SingletonHolder被加载和被初始化,此时静态初始化器将执行Singleton的初始化操作。
排序算法
- 冒泡排序:
public static void bubbleSort(int[] array) {
if (array == null || array.length == 0) {
return;
}
for (int i = 0; i < array.length - 1; i++) {
for (int j = 0; j < array.length - i - 1; j++) {
if (array[j] > array[j + 1]) {
int temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
}
}
}
}时间复杂度:
在通常情况下。冒泡排序的比较次数 = (n - 1) + (n - 2) + ... + 2 + 1,即:n * (n - 1) / 2,所以冒泡排序的时间复杂度为:O(n^2)。
- 插入排序

public class InsertSort {
public static void insertSort(int array[]) {
if (array == null || array.length == 0) {
return;
}
for (int i = 1; i < array.length; i++) {
// 当array[i]比arra[i - 1]小时才进入处理
if (array[i] < array[i - 1]) {
// 临时变量存储array[i]的值
int temp = array[i];
// 从当前位置开始处理
int j = i;
// 将比temp大的数往后挪一个位置,为temp腾出一个合适位置
while (j > 0 && temp < array[j - 1]) {
array[j] = array[j - 1];
j--; // 填充完后, 继续向前比较
}
// 将temp放在属于它的位置上
array[j] = temp;
}
}
}
}时间复杂度:
- 在最坏的情况下,即整个数组是倒序的,比较次数 = 1 + 2 + 3 + ... + (n - 2) + (n - 1) = n * (n - 1) / 2,此时的时间复杂度为:O(n^2)。
- 在最好的情况下,即整个数组是正序的,比较次数 = n - 1,此时的时间复杂度为:O(n)。
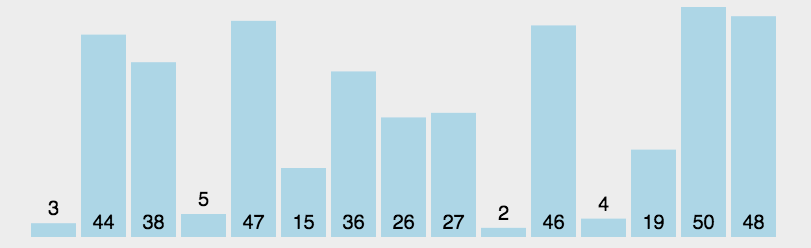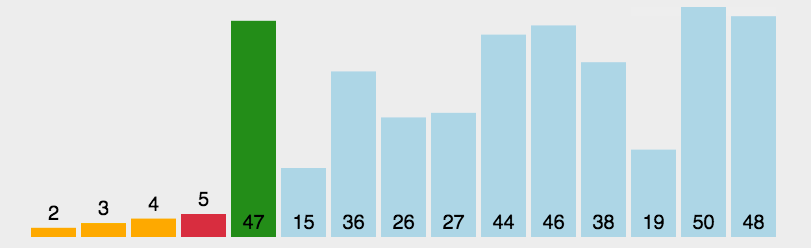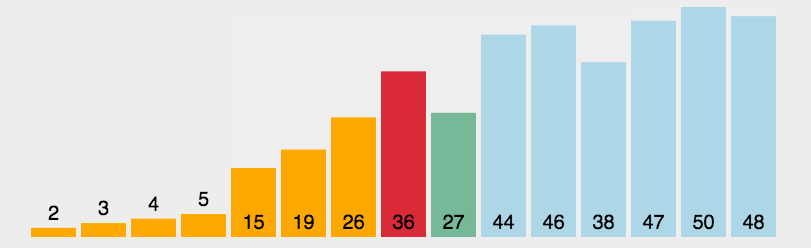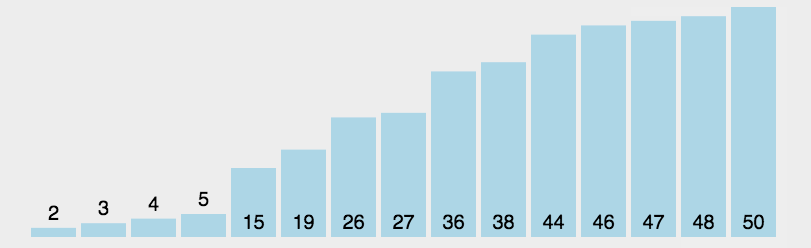
- 选择排序
public class SelectSort {
public static void selectSort(int[] array) {
if (array == null || array.length == 0) {
return;
}
for (int i = 0; i < array.length - 1; i++) {
// 记录当次遍历值最小的数的位置
int minIndex = i;
for (int j = i + 1; j < array.length; j++) {
// 如果array[j]比array[minIndex]小, 则将minIndex修改为j
if (array[j] < array[minIndex]) {
minIndex = j;
}
}
if (i != minIndex) {
// 将当次遍历的最小值交换到对应位置
int temp = array[i];
array[i] = array[minIndex];
array[minIndex] = temp;
}
}
}
}时间复杂度:
如果将数组的长度看作n,第一次循环时,j 从1开始直到n - 1,因此比较次数为n - 1;第二次为n - 2,依此类推。最终得到选择排序的比较次数 = (n - 1) + (n - 2) + ... + 2 + 1 = n * (n - 1) / 2,因此时间复杂度为:O(n^2)。
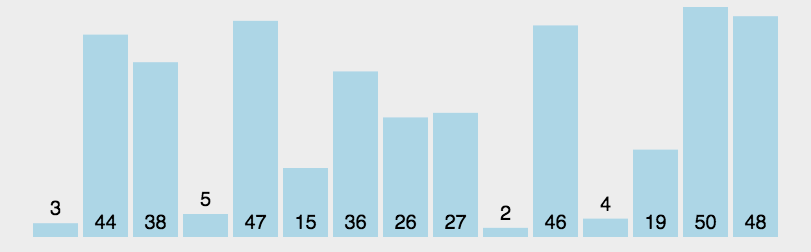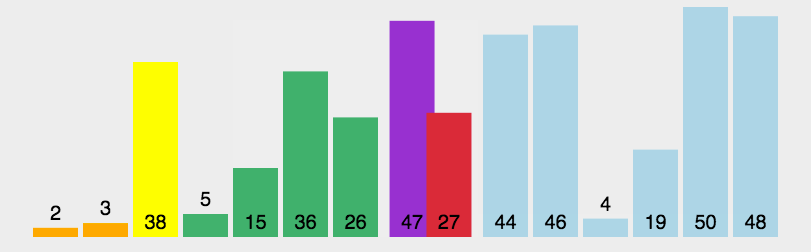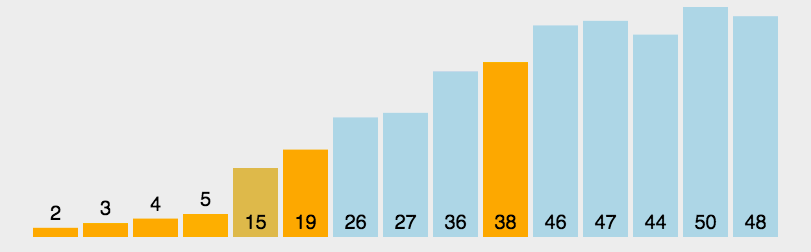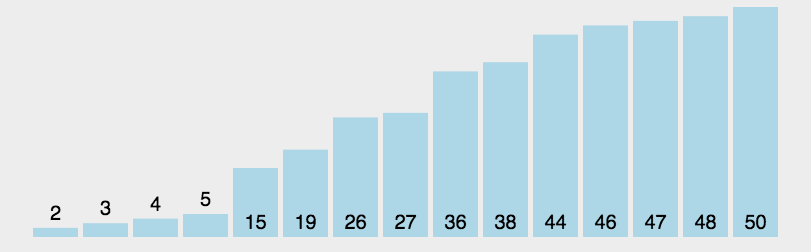
- 快速排序
public class QuickSort {
private static void quickSort(int[] array, int low, int high) {
if (low >= high) {
return;
}
int i = low, j = high, index = array[i]; // 取最左边的数作为基准数
while (i < j) {
while (i < j && array[j] >= index) { // 向左寻找第一个小于index的数
j--;
}
if (i < j) {
array[i++] = array[j]; // 将array[j]填入array[i],并将i向右移动
}
while (i < j && array[i] < index) {// 向右寻找第一个大于index的数
i++;
}
if (i < j) {
array[j--] = array[i]; // 将array[i]填入array[j],并将j向左移动
}
}
array[i] = index; // 将基准数填入最后的坑
quickSort(array, low, i - 1); // 递归调用,分治
quickSort(array, i + 1, high); // 递归调用,分治
}
public static void quickSort(int[] array) {
if (array == null || array.length == 0) {
return;
}
quickSort(array, 0, array.length - 1);
}
}时间复杂度:
- 最好情况的时间复杂度为O(nlogn)。
- 最差情况下每一次取到的数(基准数)都是当前要比较的数中的最大/最小值,在这种情况下,每次都只能得到比上一次少1个数的子序列(即要么全比基准数大,要么全比基准小),此时相当于一个冒泡排序,比较的次数 = (n - 1) + (n - 2) + ... + 2 + 1 = (n - 1) * n / 2,此时的时间复杂度为:O(n^2)。最差情况一般出现在:待排序的数据本身已经是正序或反序排好了。
- 归并排序
public class MergeSort {
public static void mergeSort(int[] array) {
if (array == null || array.length == 0)
return;
int[] temp = new int[array.length];
mergeSort(array, 0, array.length - 1, temp);
}
// 归并
private static void mergeSort(int array[], int first, int last, int temp[]) {
if (first < last) {
int mid = (first + last) / 2;
mergeSort(array, first, mid, temp); // 递归归并左边元素
mergeSort(array, mid + 1, last, temp); // 递归归并右边元素
mergeArray(array, first, mid, last, temp); // 再将二个有序数列合并
}
}
/**
* 合并两个有序数列
* array[first]~array[mid]为第一组
* array[mid+1]~array[last]为第二组
* temp[]为存放两组比较结果的临时数组
*/
private static void mergeArray(int array[], int first, int mid, int last, int temp[]) {
int i = first, j = mid + 1; // i为第一组的起点, j为第二组的起点
int m = mid, n = last; // m为第一组的终点, n为第二组的终点
int k = 0; // k用于指向temp数组当前放到哪个位置
while (i <= m && j <= n) { // 将两个有序序列循环比较, 填入数组temp
if (array[i] <= array[j])
temp[k++] = array[i++];
else
temp[k++] = array[j++];
}
while (i <= m) { // 如果比较完毕, 第一组还有数剩下, 则全部填入temp
temp[k++] = array[i++];
}
while (j <= n) {// 如果比较完毕, 第二组还有数剩下, 则全部填入temp
temp[k++] = array[j++];
}
for (i = 0; i < k; i++) {// 将排好序的数填回到array数组的对应位置
array[first + i] = temp[i];
}
}
}时间复杂度:
归并排序的时间复杂度为O(nlogn)。